「每日一题」力扣 147 对链表进行插入排序

你好啊，我是蓝莓，今天是每日一题的第 45 天。

题目清单：一起刷力扣 (opens new window)

引用力扣题目：147 对链表进行插入排序 (opens new window)

题目描述

给定单个链表的头 head ，使用 插入排序 对链表进行排序，并返回 排序后链表的头 。

插入排序 算法的步骤:

1. 插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
2. 每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
3. 重复直到所有输入数据插入完为止。

下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时，从输入数据中删除一个元素(红色)，并就地插入已排序的列表中。

对链表进行插入排序。

示例 1：

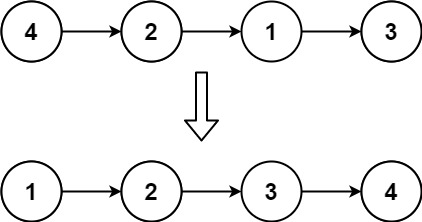
输入: head = [4,2,1,3]
输出: [1,2,3,4]

示例 2：

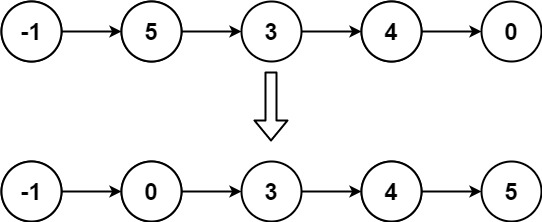
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]

提示：

• 列表中的节点数在 [1, 5000]范围内
• -5000 <= Node.val <= 5000

实现

思路

• 在数组上使用插入排序的时候，每次插入一个数值，我们都需要把插入点和后面的数值全部向后移动一个位置，然后空出来这个插入点的位置才能让我们插入
• 所以这主要还是一个链表的基础操作，就是插入一个节点
• 在寻找插入点的时候，我们可以注意这么两个条件（按照递增排序）
• （1）如果当前待插入节点的值大于等于当前遍历到的插入点的值，那么就继续向后遍历，否则停下来
• （2）如果当前遍历到的这个节点已经超出了排序完成的区间范围，那么就停下来（这一点可以通过：当前的节点的是不是当前待插入节点这一条件来判断）
• 好了，明确了以上两个问题我们再来看一下如何插入一个节点
• 我们要插入的这个节点本身就是链表中的，所以我们需要先把这个节点给取下来，这个过程就已经需要我们来维护当前节点的前一个节点的 next 指针的指向了，所以我们需要一个 pre 来记录当前的节点 cur 的前一个节点是谁
• 那么，同时，我们还需要维护插入位置的前一个节点的指针的指向，为了减少变量的使用，我直接用一个 search 来代表插入位置的前一个节点了，与此同时我们通过 search->next 也可以访问到当前需要比较大小的那个插入点位置的节点的 val ；当然了，你也可以再添加一个变量，或许用着方便一些
• 最后就是维护一下 cur 指针指向的那个节点，如果我们需要将这个节点插入到一个为止，那么 cur 的 next 指针也需要维护一下

C++ 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        ListNode* dummyHead = new ListNode(-1, head);

        ListNode* pre = dummyHead;
        ListNode* cur = head;

        while( cur != nullptr ) {
            // search 指向比较元素的前一个节点
            ListNode* search = dummyHead;

            while( cur->val >= search->next->val && search->next != cur ) {
                search = search->next;
            }

            if( search->next != cur ) {
                // 这时候执行插入逻辑
                ListNode* searchNext = search->next;
                ListNode* curNext = cur->next;
                search->next = cur;
                cur->next = searchNext;
                pre->next = curNext;  // pre 不需要移动
                cur = pre->next;  // 此时应该更新 cur
            } else {
                // 这说明应当插入在已经排序完成的所有节点的后面
                // 那说明 cur 当前所处位置就是正确的 直接跳过即可
                pre = cur;
                cur = cur->next;
            }
        }

        cur = dummyHead->next;
        delete dummyHead;
        
        return cur;
    }
};