「每日一题」力扣 102 二叉树的层序遍历

你好啊，我是蓝莓，今天是每日一题的第 54 天。

题目清单：一起刷力扣 (opens new window)

引用力扣题目：102 二叉树的层序遍历 (opens new window)

题目描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

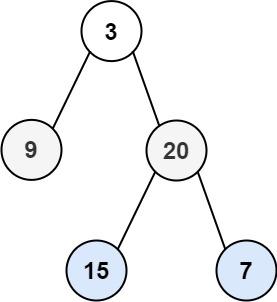
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

实现

思路

• 这是一个力扣的中等题
• 这是数据结构中的广度优先基础方法
• 只是在我们进行广度优先搜索的过程中要想个办法明确当前遍历的是哪一层，因为我们的节点一旦放入队列中后，我们就不知道这个节点是不是不属于我们正在遍历的那一层了
• 但是，你可以明确的知道，二叉树的最上层只有一个根节点，在你遍历这一层的时候，你通过判断它这个节点的左子树和右子树是否为空的情况时，也就知道了下一层有多少个节点了，其实当你遍历完当前这一层的时候，队列中装进去的刚好就是下一层的所有节点
• 好啦，那么具体的逻辑看代码就懂啦

C++ 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // q 队列用于辅助广度优先搜索
        queue<TreeNode*> q;
        // res 里面的每一个 vector<int> 用来存储一层的元素
        vector<vector<int>> res;

        // 如果这是一个空二叉树 直接返回空的 res 即可
        if( root == nullptr ) {
            return res;
        }

        // 为把第一层的元素装进去做准备
        res.push_back(vector<int>());

        int level = 0;  // 当前正在遍历的层（自顶向下从 0 开始）
        int nodeNums = 1;  // 当前层的节点数量
        q.push(root);  // 将 root 节点放入队列中

        while(!q.empty()) {
            TreeNode* node = q.front();
            q.pop();

            // 若左子树不为空则将左子树的根节点放入队列中
            if( node->left != nullptr ) {
                q.push(node->left);
            }

            // 若右子树不为空则将右子树的根节点放入队列中
            if( node->right != nullptr ) {
                q.push(node->right);
            }

            // 将当前遍历的节点的值放入 level 层的 vector<int> 中
            res[level].push_back(node->val);
            nodeNums--;  // 将当前层的节点计数减少 1
            
            // 如果当前层已经遍历完了 并且 队列中还有元素
            // 那么维护这些变量
            if( nodeNums <= 0 && !q.empty() ) {
                level++;  // 移动到下一层
                res.push_back(vector<int>());  // 初始化下一层的 vector<int>
                nodeNums = q.size();  // 当前队列中存储的元素便是下一层的所有节点
            }
        }

        return res;
    }
};