「每日一题」力扣 149 直线上最多的点数

你好啊，我是蓝莓，今天是每日一题的第 31 天。

题目清单：一起刷力扣 (opens new window)

引用力扣题目：149 直线上最多的点数 (opens new window)

题目描述

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例 1：

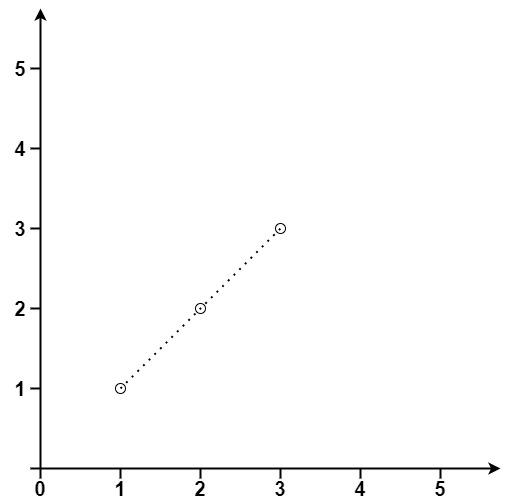
输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例 2：

输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

提示：

• 1 <= points.length <= 300
• points[i].length == 2
• -10^4 <= xi, yi <= 10^4
• points 中的所有点 互不相同

实现

思路

• 我们都知道两点确定一条直线
• 先确定一个点，然后求该点和其他所有点构成直线的斜率，使用求得的斜率作为哈希表的 key ，使用落在该斜率上的点的数量作为哈希表的值
• 现在最大的问题是，斜率是一个小数，但是在计算机中只有浮点数，所以是有误差的，不太能作为哈希表的键
• 另一种斜率表示法：我们可以使用比值的方式存储斜率，只需要将该分数的分子和分母化为最简就可以了，这样一来，我们就可以使用两个整型精确的表示一个分数了
• 设 a 为该分数的分子，b为该分数的分母，为了统一，若该分数为负数，我们总是让负号出现在 b 中
• 根据题目提供的信息我们可以知道
• （1）表示斜率的分子被我们统一成了整数，结合每个点的坐标范围，我们可以计算出斜率的分子 a 的范围是 0 到 2 × 10^4
• （2）表示斜率的分母 b 可正可负，所以分母的取值范围是 -2 × 10^4 到 2 × 10^4
• 最后，我们使用一个 32 位的整数来保存这两个内容，我们让 b 乘以 2 × 10^4 + 1 这样一来，我们就在数轴的中间部分空出了很大一部分的空间，我们让这个数值再加上 a ，这样一来，我们总是可以通过两个值的和得到唯一的 键

C++ 代码实现

class Solution {
public:

    int _gcd(int a, int b) {
        if( b == 0 ) {
            return a;
        }

        return _gcd(b, a%b);
    }

    int gcd(int a, int b) {
        if( a == b ) {
            return a;
        }

        return _gcd(max(a, b), min(a, b));
    }

    int maxPoints(vector<vector<int>>& points) {
        // 对每一个点 i;
        // record[i] 记录其他点到该点不同斜率收集的点的数量
        // record[i][斜率] = 数量
        int res = 0;

        for( int i = 0 ; i < points.size() ; i++ ) {

            unordered_map<int, int> record; 
            for( int j = 0 ; j < points.size() ; j++ ) {
                if( i == j ) continue;

                int a = points[i][0] - points[j][0];
                int b = points[i][1] - points[j][1];

                if( a == 0 ) {
                    b = 1;
                } else if( b == 0 ) {
                    a = 1;
                } else {
                    
                    if( a < 0 ) {
                        a = -a;
                        b = -b;
                    }
                    int ab_gcd = gcd(abs(a), abs(b));

                    a = a / ab_gcd;
                    b = b / ab_gcd;
                }

                // 从数轴上可以观察到这样不会产生冲突
                int key = 20001 * b + a;
                record[key] ++;
            }

            for( auto iter = record.begin() ; iter != record.end() ; iter++ ) {
                res = max(res, iter->second);
            }
        }

        return res+1;
    }
};